Advertisements
Advertisements
Question
Find the area of the region bounded between the curves y = sin x and y = cos x and the lines x = 0 and x = π
Solution
First find the intersecting point of two curves
sin x = cos x
tan x = 1
x = `pi/4`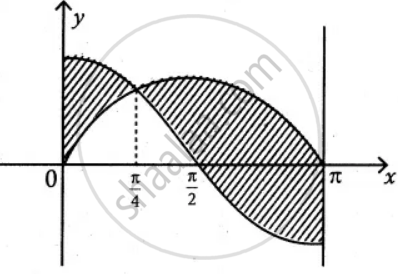
Area required = `int_0^(pi/4) (cos x - sin x) "d"x + int_(pi/4)^pi (sin x - cos x) "d"x`
= `[sin x + cos x]_0^(pi/4) + [- cos x - sin x]_(pi/4)^pi`
= `[1/sqrt(2) + 1/sqrt(2) - 1] + [1 + 1/sqrt(2) + 1/sqrt(2)]`
= `4/sqrt(2)`
= `2sqrt(2)` sq.units
Area required = `2sqrt(2)` sq.units
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by 3x – 2y + 6 = 0, x = – 3, x = 1 and x-axis
Find the area of the region bounded by 2x – y + 1 = 0, y = – 1, y = 3 and y-axis
Find the area of the region bounded by the curve 2 + x – x2 + y = 0, x axis, x = – 3 and x = 3
Find the area of the region bounded by the line y = 2x + 5 and the parabola y = x2 – 2x
Find the area of the region bounded by y = tan x, y = cot x and the lines x = 0, x = `pi/2`, y = 0
Find the area of the region bounded by the parabola y2 = x and the line y = x – 2
The curve y = (x – 2)2 + 1 has a minimum point at P. A point Q on the curve is such that the slope of PQ is 2. Find the area bounded by the curve and the chord PQ
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x
Choose the correct alternative:
The area between y2 = 4x and its latus rectum is
Choose the correct alternative:
If `int_0^"a" 1/(4 + x^2) "dx=pi/8` then a is
