Question

Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`

Options

• `21/2` sq.units

• `36/5` sq.units

• 21 sq.units

• None of the these

Answer 1

`21/2` sq.units

Explanation:

Equation of the parabola is,

`y = x^2 + 2` or `x^2 = (y - 2)`

Its vertex is (0, 2) Axis is `y`-axis.

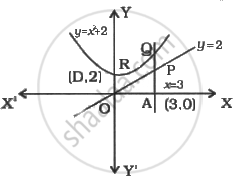
Boundary lines are `y = x, x = 0, x = 3`

Graphs of the curve and lines have been shown in fig area of the region PQRO

Area of the region OAQR - Area of region OAP.

= `int_0^3 (x^2 + 2)dx - int_0^3 xdx`

= `[x^3/3 + 2x]_0^3 - [x^2/2]_0^3`

= `[(27/3 + 6) - 0] - (9/2 - 0)`

= `15 - 9/2`

= `21/2` sq.unit