Question

Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.

Options

• `14/3` sq.units

• `8/3` sq.units

• 16 sq.units

• None of these

Answer 1

`14/3` sq.units

Explanation:

The curve `y^2 = x` is a parabola with vertex at origin. Axis of `x` is the line of symmetry which is the axis of parabola.

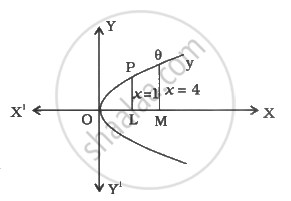
The area of the region bounded by the curve `x` = 1, `x` = 4 and the `x`-axis.

= Area ∠MQP = `int_1^4 ydx = int_1^4 sqrt(x) dx`

= `2/3[x^(3/2)]_1^4`

= `2/3[4^(3/2) - 1^(3/2)]`

= `2/3[8 - 1]`

= `14/3` sq.units.