Question

Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.

Options

• `4sqrt(2)` sq.units

• `(16 - 4sqrt(2))` sq.units

• `(4sqrt(2) - 16)` sq.units

• `(16 + 4sqrt(2))` sq.units

Answer 1

`(16 - 4sqrt(2))` sq.units

Explanation:

The given curve is `y^2 = 9x`,

This is a parabola with parts at (0, 0) and an axis parallel to the `x`-axis. It is symmetrical about the `x`-axis because it only contains even powers of `y`, and `x` = 2 and `x` = 4 are straight lines parallel to the `y`-axis at positive distances of 2 and 4 units from it, respectively.

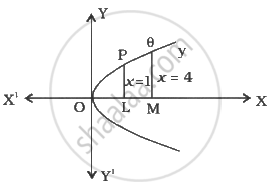
∴ Required area = area ABCD

= `int_0^3 (x^2 + 2)dx - int_0^3 xdx`

= `[x^3/3 + 2x]_0^3 - [x^2/2]_0^3`

`[because y^2 = 9x => y = +-3 sqrt(x),  "for upper portion", y = 3sqrt(x)]`

= `3 xx [x^(3/2)/(3/2)]_2^4`

= `3 xx 2/3[x^(3/2)]_2^4`

= `2[4^(3/2) - 2^(3/2)]`

= `2[8 - 2sqrt(2)]`

= `(16 - 4sqrt(2))` sq.units.