Question

Find the combined equation of the pair of lines through the origin and making an angle of 30° with the line 2x – y = 5

Answer 1

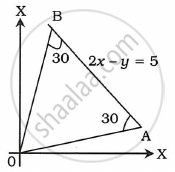
Let OA or OB be the line making an angle of 30° with 2x – y = 5

Let the equation of OA be y = mx   ....(1)

Using 

tan θ = `|(m_1 - m_2)/(1 + m_1m_2)|`

where θ = 30°, m₁ = m, m₂ = 2

∴ tan 30° = `|(m - 2)/(1 + 2m)|`

`1/sqrt(3) = |(m - 2)/(1 + 2m)|`

 Squaring both sides

`1/3 = (m - 2)^2/(1 + 2m)^2`

∴ 1 + 4m + 4m² = 3m² – 12m + 12

∴ m² + 16m – 11 = 0

Put m = `y/x` (From (1))

∴ `y^2/x^2 + (16y)/x - 11` = 0

∴ 11x² – 16xy – y² = 0