Question

Find the dimensions of the rectangle with maximum area that can be inscribed in a circle of radius 10 cm

Answer 1

Let the length of the rectangle be ‘x’ cm

The breadth of the rectangle be ‘y’ cm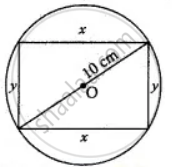

From the figure,

x² + y² = (20)²  ......[Pythagoras Theorem]

y² = 400 – x² ......[∵ radius of the circle is 10 cm]

y = `sqrt(400 - x^2)`

Now, Axea of the rectangle A = xy

A = `xsqrt(400 - x^2)`

`"dA"/("d"x) = x  ((- 2x))/(2sqrt(400 - x^2)) + sqrt(400 - x^2) (1)`

= `(- x^2 + 400 - x^2)/sqrt(400 - x^2)`

= `(- 2x^2 + 400)/sqrt(400 - x^2)`

For maximum or minimum,

`"dA"/("d"x)` = 0

⇒ `(- 2x^2 + 400)/sqrt(400 - x^2)`

x² = 200

x = `+-   10sqrt(2)`

x = `-  10sqrt(2)` is not possible

∴ x = `10sqrt(2)`

Now, `("d"^2"A")/("d"x^2) = (sqrt(400 - x^2)(- 4x) - (- 2x^2 + 400) (- (2x)/(2sqrt(400 - x^2))))/(400 - x^2)`

= `(2x^3 - 1200x)/((400 - x^2)sqrt(400 - x^2))`

At x = `10sqrt(2), ("d"^2"A")/("d"x^2) < 0`

Area of the rectangle is maximum

When x = `10sqrt(2)`

y = `sqrt(400 - 200)`

= `sqrt(200)`

= `10sqrt(2)`

∴ x = y = `10sqrt(2)`

Length of the rectangle = `10sqrt(2)` cm

Breadth of the rectangle = `10sqrt(2)` cm