Question

Find the equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes.

Answer 1

The circle passes through the origin and makes intercepts on the axes a, b.

OA = a,

∴ Coordinates of A (a, 0)

OB = b,

∴ Coordinates of B (0, b)

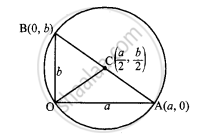
⇒ Coordinates of the center `(("a" + 0)/2, (0 + "b")/2)` or `("a"/2, "b"/2)`

radius OC = `sqrt(("a"/2 - 0)^2 + ("b"/2 - 0)^2)` 

= `sqrt(("a"^2 + "b"^2)/4)`

= `sqrt("a"^2 + "b"^ 2)/2`

∴ equation of circle

`("x" - "a"/2)^2 + ("y" - "b"/2)^2`

= `(sqrt("a"^2 + "b"^ 2)/2)^2`

or `"x"^2 - "ax" + "a"^2/4 + "y"^2 - "by" + "b"^2/4 = ("a"^2 + "b"^2)/4`

or x² + y² – ax – by = `("a"^2 + "b"^2)/4 - ("a"^2 + "b"^2)/4`

∴ Required equation of circle

x² + y² – ax – by = 0