Advertisements
Advertisements
Question
Find the graphical solution of the following system of linear inequations:
x – y ≤ 0, 2x – y ≥ − 2
Solution
To find graphical solution, construct the table as follows:
| Inequation | Equation | Double Intercept form | Points (x, y) | Region |
| x – y ≤ 0 | x – y = 0 | - | O (0, 0) A (1, 1) |
(0) – (0) ≤ 0 ∴ 0 ≤ 0 ∴ origin side |
| 2x – y ≥ − 2 | 2x – y = − 2 | `(2"x")/-2-"y"/-2=(-2)/-2` | B (–1, 0) C (0, 2) |
2(0) – (0) ≥ –2 ∴ 0 ≥ –2 ∴ origin side |
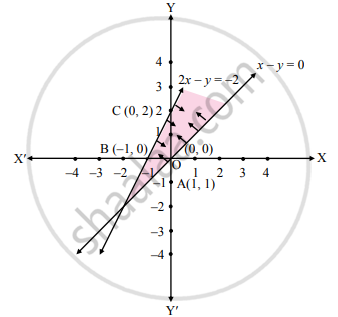
The shaded portion represents the graphical solution.
APPEARS IN
RELATED QUESTIONS
Solve the following system of inequalities graphically: 2x – y > 1, x – 2y < –1
Solve the following system of inequalities graphically: x + y ≤ 9, y > x, x ≥ 0
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically: x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solve the following system of inequalities graphically: 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Solve the following system of inequalities graphically: x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Find all pairs of consecutive odd positive integers, both of which are smaller than 10, such that their sum is more than 11.
The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of at least 65 marks.
A solution is to be kept between 30°C and 35°C. What is the range of temperature in degree Fahrenheit?
Write the set of values of x satisfying the inequations 5x + 2 < 3x + 8 and \[\frac{x + 2}{x - 1} < 4\]
Write the solution of set of\[\left| x + \frac{1}{x} \right| > 2\]
Find the graphical solution of the following system of linear inequations:
`"x"/60 + "y"/90 ≤ 1`, `"x"/120 + "y"/75 ≤ 1`, y ≥ 0, x ≥ 0
Show that the following system of linear inequalities has no solution x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Show that the solution set of the following system of linear inequalities is an unbounded region 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0.
Solution set of x ≥ 0 and y ≤ 0 is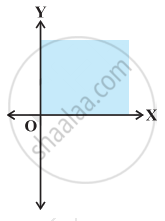
Solution set of x ≥ 0 and y ≤ 1 is