Question

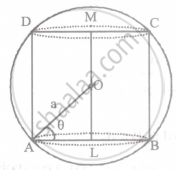
Find the height of the cylinder of maximum volume that can be inscribed in a sphere of radius a.

Options

• `(2"a")/3`

• `(2"a")/sqrt3`

• `"a"/3`

• `3/"a"`

Answer 1

`(2"a")/sqrt3`

Explanation:

Let r be the radius of the base and h be the height of the cylinder ABCD which is inscribed in a sphere of radius a. It is obvious that for maximum volume the axis of the cylinder must be along the diameter of the sphere. Let O be the centre of the sphere such that OL = x. Then OA² = OL² + AL²

Let V be the volume of cylinder. Then,

V = `pi(AL)^2 xx LM`

⇒ V = `pi(AL)^2 xx 2(OL) = pi(a^2 - x^2) xx 2x`

⇒ V = `2pi(a^2x - x^3)`

⇒ `(dV)/(dx) = 2pi (a^2 - 3x^2)`

And `(d^2V)/(dx^2) = - 12pix`

For maximum or minimum values of V, we must have `(dV)/(dx)` = 0

⇒ `2pi(a^2 - 3x^2)` = 0

⇒ `x = a/sqrt(3)`  ........`["Neglecting"  x = (-a)/sqrt(3)  because ((d^2V)/(dx^2))_(x = (-a)/sqrt(3)) > 0]`

Clearly, `((d^2V)/(dx^2))_(x = a/sqrt(3)) = - 12pi xx a/sqrt(3) < 0`

∴ . V is maximum when x = `a/sqrt(3)`

Hence, height of the cylinder LM = `2x = (2a)/sqrt(3)`