Question

Find the interval in which the function `f` is given by `f(x) = 2x^2 - 3x` is strictly decreasing.

Options

• `(3/2, oo)`

• `(- oo, 3/4)`

• `(- oo, oo)`

• `(0, oo)`

Answer 1

`(- oo, 3/4)`

Explanation:

`f(x) = 2x^2 - 3x`

∴ `f^1(x) = 4x - 3`

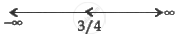
`f^'(x) = 0` at `x = 3/4`

The point `x = 3/4` divides the real lines into two disjoint intervals Viz `(- oo, 3/4)` and `(3/4, oo)`.

In the interval, `f^'(x)` is negative, therefore `f` is strictly decreasing in `(- oo, 3/4)`.