Advertisements
Advertisements
Question
Find the range of values of x which satisfies
`-2 2/3 <= x + 1/3 < 3 1/3, x in R`
Graph these values of x on the number line.
Solution
`-2 2/3 <= x + 1/3 and x + 1/3 < 3 1/3`
`=> -8/3 <= x + 1/3 and x +1/3 < 10/3 `
`=> -8/3 - 1/3 <= x and x < 10/3 - 1/3`
`=> -9/3 <= x and x < 9/3`
`=> -3 <= x and x < 3`
`∴ -3 <= x < 3`
The required graph of the solution set is
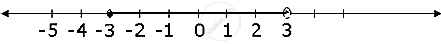
APPEARS IN
RELATED QUESTIONS
If the replacement set is the set of whole numbers, solve:
8 – x > 5
If the replacement set is the set of real numbers, solve:
8 – 3x ≤ 20
If the replacement set is the set of real numbers, solve:
`5 + x/4 > x/5 + 9`
Find the values of x which satisfy the inequation:
`-2 <= 1/2 - (2x)/3 ≤ 1 5/6; x ∈ N`
Graph the solution on the number line.
Solve for x in the following in equation, if the replacement set is N<10:
x + 5 > 11
Solve for x in the following in equation, if the replacement set is N<10:
8 - 3x > 2
Solve for x in the following in equation, if the replacement set is N<10:
5 - 2x < 11
If x + 17 ≤ 4x + 9, find the smallest value of x, when:
x ∈ Z
Solve the following inequation and graph the solution set,
2x -3 ≤ x + 2 ≤ 3x + 5 x ∈ R.
Find the solution set of the following inequalities and draw the graph of their solutions sets:
`(3)/|x - 2| > 5`.
