Advertisements
Advertisements
Question
Find the smallest square number which is divisible by each of the numbers 6, 9, and 15.
Sum
Solution
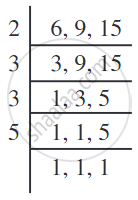
The least number divisible by each one of 6, 9, and 15 is their LCM.
The LCM of 6, 9 and 15 is 2 × 3 × 3 × 5 = 90.
Prime factorisation of 90 is 90 = 2 × 3 × 3 × 5.
The prime factors 2 and 5 are not in pairs. Therefore 90 is not a perfect square.
In order to get a perfect square, each factor of 90 must be paired. So we need to
make pairs of 2 and 5. Therefore, 90 should be multiplied by 2 × 5, i.e., 10.
Hence, the required square number is 90 × 10 = 900.
shaalaa.com
Is there an error in this question or solution?
