Question

For real number a, b (a > b > 0),

let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π

Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.

Then the value of (a – b)² is equal to ______.

Options

• 11

• 12

• 13

• 14

Answer 1

For real number a, b(a > b > 0),

let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π

Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.

Then the value of (a – b)² is equal to 12.

Explanation:

Given: Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π

And area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 18π

Case-1

x² + y² ≤ a² represents the region inside the circle x² + y² = a²

`x^2/a^2 + y^2/b^2 ≥ 1` represents the region outside the ellipse `x^2/a^2 + y^2/b^2` = 1

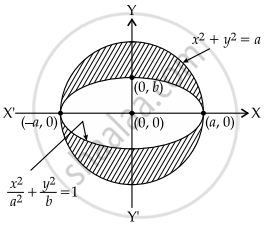
Now, shaded area = πa² – πab = 30π

⇒ a² = 30 + ab  ...(i)

Case-2

x² + y² ≥ b² represents the reigon outside the circle x² + y² = b²

`x^2/a^2 + y^2/b^2 ≤ 1` represents the region inside the ellipse `x^2/a^2 + y^2/b^2` = 1.

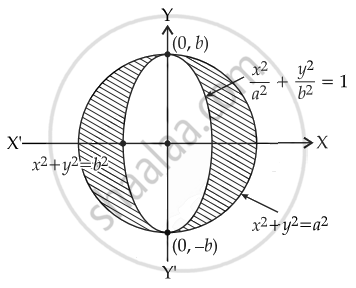
Now, shared area = πab – πb² = 18π

⇒ b² = ab – 18  ...(ii)

Adding equation (i) and equation (ii), we get

a² + b² = 2ab + 12

⇒ (a – b)² = 12