Advertisements
Advertisements
Question
For the same objective, find the ratio of the least separation between two points to be distinguished by a microscope for light of 5000 Å and electrons accelerated through 100 V used as the illuminating substance.
Solution
Resolving power is the ability of an imaging device to separate (i.e., to see as distinct) points of an object that are located at a small angular distance or it is the power of an optical instrument to separate far–away objects, that are close together, into individual images. The term resolution or minimum resolvable distance is the minimum distance between distinguishable objects in an image, although the term is loosely used by many users of microscopes and telescopes to describe resolving power. In scientific analysis, in general, the term “resolution” is used to describe the precision with which any instrument measures the Ratio of the least separation,
For electrons accelerated through 100 V, the de-Broglie wavelength, is 12.27 and records (in an image or spectrum) any variable in the specimen or sample under study.
It is defined as the reciprocal of the smallest distance (Δx) between two point objects whose images are just resolved by the objective of the microscope. It is given by `R = 1/(Δx) = (2 sin α)/(1.22 μλ)` where μ as refractive index of the medium, α is the angle subtended by the objective at the object and λ is the wavelength of light.
de-Broglie wavelength: According to de-Broglie theory, the wavelength of de-Broglie wave is given by `lambda = h/p = h/(mv) = h/sqrt(2mE)` ⇒ `lambda oo 1/p oo 1/v oo 1/sqrt(E)` where h = Planck's constant, m = Mass of the particle, v = Speed of the particle, E = Energy of the particle.
The energy of a charged particle accelerated through potential difference V is `E = 1/2 mv^2 = qV`
Hence de-Broglie wavelength `lambda = h/p = h/sqrt(2mE) = h/sqrt(2mqV)`
For electron, `λ_("Electron") = 12.27/sqrt(V) Å`
We know that
Resolving power = `1/d = (2 sin α)/(1.22 λ)` ⇒ `d_("min") = (122 λ)/(2 sin α)`
Where λ is the wavelength of light and β is the angle subtended by the objective at the object.
For the light of wavelength 5500 Å,
`d_("min") = (1.22 xx 5500 xx 10^-10)/(2 sin α)` .......(i)
For electrons accelerated through 100 V, the de-Broglie wavelength,
`λ = 12.27/sqrt(V) = 12.27/sqrt(100) = 0.12 xx 10^-9 m`
`d_("min") = (122 xx 0.12 xx 10^-9)/(2 sin α)`
Ratio of the least separation, `d_("min")^'/d_("min") = (0.12 xx 10^-9)/(5500 xx 10^-10) = 0.2 xx 10^-3`
APPEARS IN
RELATED QUESTIONS
For a glass plate as a polariser with refractive index 1.633, calculate the angle of incidence at which light is polarised.
Three identical polaroid sheets P1, P2 and P3 are oriented so that the pass axis of P2 and P3 are inclined at angles of 60° and 90° respectively with the pass axis of P1. A monochromatic source S of unpolarised light of intensity I0 is kept in front of the polaroid sheet P1 as shown in the figure. Determine the intensities of light as observed by the observer at O, when polaroid P3 is rotated with respect to P2 at angles θ = 30° and 60°.
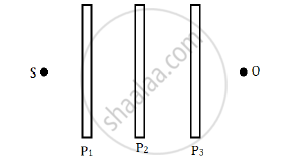
Two polaroids P1 and P2 are placed with their pass axes perpendicular to each other. An unpolarised light of intensity Io is incident on P1. A third polaroid P3 is kept in between P1 and P2 such that its pass axis makes an angle of 45° with that of P1. Determine the intensity of light transmitted through P1, P2 and P3
A ray of light is incident on a transparent medium at a polarizing angle. What is the angle between the reflected ray and the refracted ray?
What is the difference between polarised light and unpolarised light?
What is plane polarised light?
State and obtain Malus’ law.
What is the angle of polarisation and obtain the equation for an angle of polarisation?
What is normal focusing?
The reflected light is found to be plane polarised when an unpolarized light falls on a denser medium at 60° with the normal. Find the angle of refraction and critical angle of incidence for total internal reflection in the denser to rarer medium reflection.
