Question

Four identical particles of equal masses 1 kg made to move along the circumference of a circle of radius 1 m under the action of their own mutual gravitational attraction. The speed of each particle will be ______.

Options

• `sqrt(((1+2sqrt2)"G")/2)`

• `sqrt("G"(1+2sqrt2)`

• `sqrt("G"/2(2sqrt2-1)`

• `sqrt("G"/4(1+2sqrt2)`

Answer 1

Four identical particles of equal masses 1 kg made to move along the circumference of a circle of radius 1 m under the action of their own mutual gravitational attraction. The speed of each particle will be `bbsqrt("G"/4(1+2sqrt2)`.

Explanation:

There are three gravitational forces on each masses.

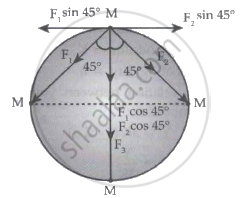
So, F_g = F₁ cos 45° + F₂ cos 45° + F₃

⇒ F_g = `(2"GMM")/(("R"sqrt2)^2) cos45° + "GMM"/(2"R")^2`

⇒ F_g = `(2"GMM")/((2"R"^2sqrt2)) + "GMM"/(4"R"^2)`

⇒ F_g = `("GM"^2)/"R"^2 (1/sqrt2 +1/4)`

This gravitational force will be balanced by centripetal force.

Hence, `("GM"^2)/"R"^2 (1/sqrt2 +1/4) = ("Mv"^2)/"R"`

v² = `("GM")/"R" (1/4+1/sqrt2 )`

⇒ v = `sqrt(("GM")/"R" (1/4+1/sqrt2 ))`

As per the question,

M = 1 kg

R = 1 m

So, v = `sqrt("G" (1/4+1/sqrt2 ))`

⇒ v = `sqrt(("G"(1+2sqrt2))/4)`

⇒ v = `sqrt("G"/4(1+2sqrt2)`