Advertisements
Advertisements
Question
Four rounds of wire fence have to be put around a field. If the field is 60 m long and 40 m wide, how much wire will be needed?
Solution
Perimeter of rectangular field
= 2 x length + 2 x breadth
= 2 x 60 + 2 x 40
= 120 + 80
= 200 m
Hence, wire required for 4 rounds.
= 200 x 4 = 800 m
∴ Wire required for 4 rounds = 800 m.
RELATED QUESTIONS
Find the perimeter of a rectangle whose:
length = 8 m and breadth = 80 cm
Each side of a square field is 70 cm. How much distance will a boy walk in order to make?
(i) one complete round of this field?
(ii) 8 complete rounds of this field?
The length of a rectangle is twice of its breadth. If its perimeter is 60 cm, find its length.
A regular pentagon of each side 12 cm has same perimeter as that of a regular hexagon. Find the length of each side of the hexagon.
The perimeter of a square is 60 m, find:
(i) its each side its area
(ii) its new area obtained on increasing
(iii) each of its sides by 2 m.
Each side of a square tile is 60 cm. How many tiles will be required to cover the floor of a hall with length = 50 m and breadth = 36 m.

Each rectangle is made out of 12 equal squares, so all have the same area, but the length of the boundary will be different.
Which of these rectangles has the longest perimeter?
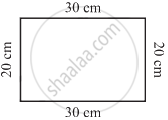
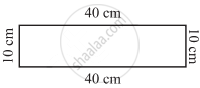
What is the perimeter of the following figures? What do you infer from the answers?
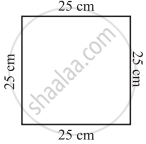 (a) |
 (c) |
 (b) |
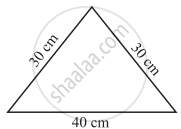 (d) |
In the given figure, perimeter of (ii) is greater than that of (i), but its area is smaller than that of (i).
 |
 |
| (i) | (ii) |
An increase in perimeter of a figure always increases the area of the figure.
