Advertisements
Advertisements
Question
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
Solution
Let BC be the tower of height h metre and CD be the water tank of height h1 metre.
Let A be a point on the ground at a distance of 40 m away from the foot B of the tower.
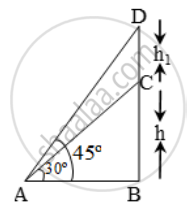
In ∆ABD, we have tan 45º = \frac { BD }{ AB }
`\Rightarrow 1=\frac{h+h_{1}}{40}\Rightarrow h+h_{1}=40\text{}m\text{ }\text{......}(i)`
In ∆ABC, we have
`\text{tan }30^\text{o}=\frac{BC}{AB}\Rightarrow\frac{1}{\sqrt{3}}=\frac{h}{40}`
`\Rightarrow h=\frac{40}{\sqrt{3}}=\frac{40\sqrt{3}}{3}=23.1\text{ m}`
Substituting the value of h in (i), we get
23.1 + h1 = 40
⇒ h1 = (40 – 23.1)m = 16.9 m
