Question

From the top of a building 60 m high, the angles of depression of the top and bottom of the vertical lamp post are observed to be 30° and 60° respectively.

1. Find the horizontal distance between the building and the lamp post.
2. Find the distance between the tops of the building and the lamp post.

Answer 1

Let the horizontal· distance between the building and lamp post is BC

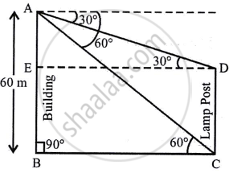
i. In ΔABC, ∠B = 90°

`tan C = (AB)/(BC)`        .... `[∵ tan theta = P/B]`

`tan 60"°" = 60/(BC)`

⇒ `sqrt3 = 60/(BC)`

BC = `60/sqrt3 xx sqrt3/sqrt3`

⇒ BC = `(60sqrt3)/3`

BC = `20sqrt3`

ii. ED = BC = `20sqrt3` m      ...(Distance between two parallel lines)

In ΔAED, ∠AED = 90°

`cos D = (ED)/(AD)`        ...`[∵ cos theta = B/H]`

`cos 30"°" = (20sqrt3)/(AD)`

⇒ `sqrt3/2 = (20sqrt3)/(AD)`

AD = 40m