Question

From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower

Answer 1

Let AB be the cliff and CD be the tower.

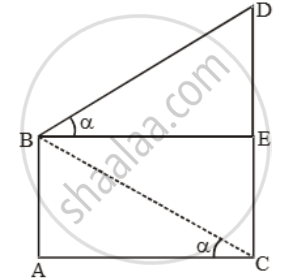
Then, AB = 25 m. From B draw BE ⊥ CD.

Let ∠EBD = ∠ACB = α.

`\text{Now, }\frac{\text{DE}}{\text{BE}}=\text{tan }\alpha \text{ and }\frac{\text{AB}}{\text{AC}}=\text{tan }\alpha \text{ } `

`\therefore \frac{DE}{BE}=\frac{AB}{AC}\text{ }So,\text{ }DE=AB [ ∵ BE = AC]`

∴ CD = CE + DE = AB + AB = 2AB = 50m