Advertisements
Advertisements
Question
Given `overline"AB"` of length 3.9 cm, construct `overline"PQ"` such that the length of `overline"PQ"` is twice that of `overline"AB"`. Verify by measurement.

(Hint: construct `overline"PX"` such that length of `overline"PX"` = length of `overline"AB"`; then cut off `overline"XQ"` such that `overline"XQ"` also has the length of `overline"AB"`.)
Solution
A line segment `overline"PQ"` can be drawn such that the length of `overline"PQ"` is twice that of `overline"AB"` as follows.
- Draw a line l and mark a point P on it and let AB be the given line segment of 3.9 cm.


- By adjusting the compasses up to the length of AB, draw an arc to cut the line at X, while taking the pointer of compasses at point P.
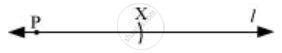
-
Again put the pointer on point X and draw an arc to cut line l again at Q.

`overline"PQ"` is the required line segment. By ruler, the length of `overline"PQ"` can be measured which comes to 7.8 cm.
APPEARS IN
RELATED QUESTIONS
Draw any circle and mark points A, B and C such that
- A is on the circle.
-
B is in the interior of the circle.
- C is in the exterior of the circle.
Draw a line segment of length 7.3 cm using a ruler.
Construct a line segment of length 5.6 cm using ruler and compasses.
Construct `overline"AB"` of length 7.8 cm. From this, cut off `overline"AC"` of length 4.7 cm. Measure `overline"BC"`.
Given `overline"AB"` of length 7.3 cm and `overline"CD"` of length 3.4 cm, construct a line segment `overline"XY"` such that the length of `overline"XY"` is equal to the difference between the lengths of `overline"AB"` and `overline"CD"`. Verify by measurement.
