Advertisements
Advertisements
Question
Given three identical Boxes A, B and C, Box A contains 2 gold and 1 silver coin, Box B contains 1 gold and 2 silver coins and Box C contains 3 silver coins. A person choose a Box at random and takes out a coin. If the coin drawn is of silver, find the probability that it has been drawn from the Box which has the remaining two coins also of silver.
Solution
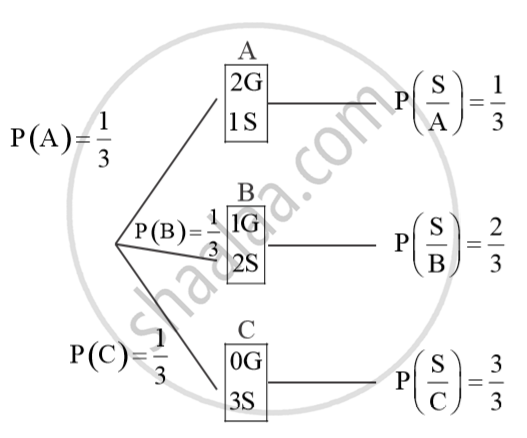
Using Baye’s theorem
`therefore P(C/S) = P(C)xx(P(S/C))/(P(A)xxP(B)xxP(S/B)+P(C)xxP(S/C))`
= `(1/3 xx 3/3)/(1/3xx1/3+1/3xx2/3 +1/3xx3/3)`
= `1/(1/3+2/3+3/3`
= `1/(6/3)`
`1/2`
APPEARS IN
RELATED QUESTIONS
Evaluate : `int sec^2x/(cosec^2x)dx`
Evaluate: `int_0^x (xtan x)/(sec x + tan x) dx`
Evaluate: `int 1/"x"^2 "sin"^2 (1/"x") "dx"`
Evaluate: `int_0^(pi/4) "log" (1 + "tan" theta) "d" theta`
Evaluate: ` int tan^3x "dx"`
Using De Moivre’s theorem, find the least positive integer n such that `((2i)/(1+i))^n` is a positive integer.
