Question

If A (5, –1), B(–3, –2) and C(–1, 8) are the vertices of triangle ABC, find the length of median through A and the coordinates of the centroid.

Answer 1

Let AD be the median through the vertex A of ∆ABC. Then, D is the mid-point of BC. So, the coordinates of

${\displaystyle (\frac{-3-1}{2}, \frac{-2+8}{2})}$

${\displaystyle \therefore AD=\sqrt{{(5+2)}^2+{(-1-3)}^2}=\sqrt{49+16}=\sqrt{65}}$

Let G be the centroid of ∆ABC. Then, G lies on median AD and divides it in the ratio 2 : 1. So, coordinates of G are

${\displaystyle (\frac{2\times (-2)+1\times 5}{2+1}, \frac{2\times 3+1\times (-1)}{2+1})}$

${\displaystyle =(\frac{-4+5}{3}, \frac{6-1}{3})=(\frac{1}{3},\frac{5}{3})}$

Application Of Section Formula

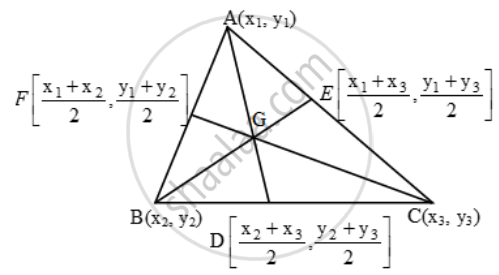
The coordinates of the centroid of the triangle whose vertices are ${\displaystyle (x_1,y_1),(x_2,y_2)}$

${\displaystyle (\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$