Question

If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.

Answer 1

Let D be the mid-point of BC. Then, the coordinates of D are (4, 0).

`∴ "Area os " triangleABC = 1/2|(4xx(-2)+3xx2+5xx(-6))-(3xx(-6)+5xx(-2)+4xx2)|`

`⇒ "Area of "triangleABC=1/2|(-8+6-30)-(-18-10+8)|`

`⇒ "Area of "triangleABC =1/2|-32+20|=6" sq. units"`

Also, We have

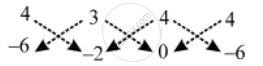
`therefore" Also of "triangle ABD =|{(4xx(-2)+3xx0+4xx(-6))}-{3xx(-6)+4xx(-2)+4xx0}|`

`⇒ "Area of "triangle ABD = 1/2|(-8+0+26)-(-18-8+0)|`

`⇒"Area of "triangle ABD =1/2|(-32+26)|=3" sq. units"`

`\Rightarrow \frac{Area\ of\ \Delta ABC}{Area\ of\ \Delta ABD}=\frac{6}{3}=\frac{2}{1}`

⇒ Area of ∆ABC = 2 (Area of ∆ABD)