Question

If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then

Options

• 9ac – 9a² – 2c² < 0

• 6ac + 9a² – 2c² < 0

• 9ac – 9a² – 2c² > 0

• 6ac + 9a² – 2c² > 0

Answer 1

9ac – 9a² – 2c² > 0

Explanation:

Radius = 3a

Length of major axis = 4c

Now, (Radius) < (Half of the length of major axis)

3a < 2c

9a² < 4c²

9ac – 9a² > 9ac – 4c²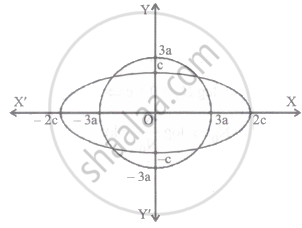 

9ac – 9a² – 2c² > 9ac – 6c²  ......(i)

Again 3a < 2c

⇒ 9ac < 6c²

⇒ 9ac – 6c² < 0   ......(ii)

From (i) and (ii),

9ac – 9a² – 2c² > 0