Question

If `bara, barb` and `barr` are position vectors of the points A, B and R respectively and R divides the line segment AB externally in the ratio m : n, then prove that `barr = (mbarb - nbara)/(m - n)`.

Answer 1

Let `bara, barb` and `barr` be the position vectors of the points A, B and R respectively w.r.t. some origin O. Then

`bar(AR)` = (p.v. of R) – (p.v. of A) = `barr - bara`

 `bar(RB)` = (p.v. of B) – (p.v. of R) = `barb - barr`

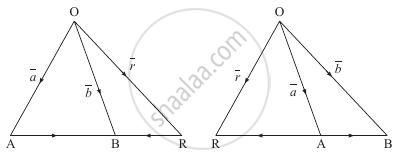
R divides seg AB externally in the ratio m : n

∴ `(AR)/(RB) = m/n`   ...(In magnitude)

∴ n · AR = m · RB and A–B–R or R–A–B

`bar(AR)` and `bar(RB)` are in opposite directions

∴ `n·(bar(AR)) = - m · (bar(RB))`

∴ `n·(barr - bara) = - m·(barb - barr)`

∴ `n·barr - n·bara = - m·barb + m·barr`

∴ `m·barb - n·bara = m·barr - n·barr`

∴ `m·barb - n·bara = (m - n)·barr`

∴ `barr = (mbarb - nbara)/(m - n)`.