Question

If a line along a chord of the circle 4x² + 4y² + 120x + 675 = 0, passes through the point (–30, 0) and is tangent to the parabola y² = 30x, then the length of this chord is ______.

Options

• 5

• `3sqrt(5)`

• 7

• `5sqrt(3)`

Answer 1

If a line along a chord of the circle 4x² + 4y² + 120x + 675 = 0, passes through the point (–30, 0) and is tangent to the parabola y² = 30x, then the length of this chord is `underlinebb(3sqrt(5))`.

Explanation:

Equation of circle 4x² + 4y² + 120x + 675 = 0

Equation of tangent to parabola y² = 30x is

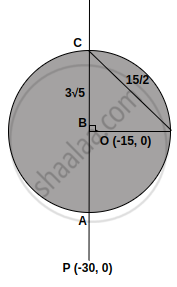
y = `"m"x + 30/(4"m")`, which passes through (–30, 0)

∴ 0 = `-30"m" + 30/(4"m")` ⇒ 4m² = 1 ⇒ m = `±1/2`

For m = `1/2` ⇒ y = `x/2 + 15` ⇒ x – 2y + 30 = 0

Length of OB = `|(-15 + 0 + 30)/sqrt(5)| = 3sqrt(5)`, radius of circle = `15/2`

Length of BC = `sqrt(225/4 - 45)` ⇒ BC = `(3sqrt(5))/2`

Length of chord AC = `2 xx (3sqrt(5))/2 = 3sqrt(5)`

Similarly, for m = `(-1)/2`, length of chord AC = `3sqrt(5)`