Question

If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`

Answer 1

∆ABD is an equilateral triangle.

We are given that AB = BC = CA = a.

AD is the altitude, i.e., AD ⊥ BC.

Now, in right angled triangles ABD and ACD, we have

AB = AC (Given)

and AD = AD (Common side)

∆ABD ≅ ∆ACD (By RHS congruence)

⇒ BD = CD ⇒ BD = DC = `\frac { 1 }{ 2 }BC = \frac { a }{ 2 }`

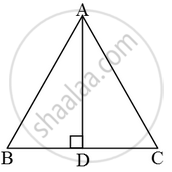
From right triangle ABD.

`AB^2 = AD^2 + BD^2`

`=>a^2=AD^2+(a/2)^2`

`AD^2=a^2-a^2/4=3/4a^2`

`\Rightarrow AD=\frac{\sqrt{3}}{2}a`