Question

If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is

`\frac{h(\tan\alpha +\tan \beta )}{\tan \beta -\tan \alpha }`

Answer 1

Let AB be the surface of the lake and let P be a point of observation such that AP = h metres. Let C be the position of the cloud and C´ be its reflection in the lake.

Then, CB = C´B. Let PM be perpendicular from P on CB. Then,

∠CPM = α and ∠MPC´= β Let CM = x.

Then, CB = CM + MB = CM + PA = x + h.

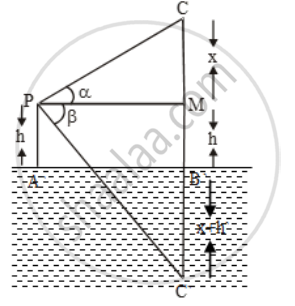
In ∆CPM, we have

`\tan \alpha =\frac{CM}{PM}`

`\Rightarrow \tan \alpha =\frac{x}{AB}`

⇒ AB = x cot α ….(i)

In ∆PMC´, we have

`\tan \beta ={C'M}/{PM}`

`\Rightarrow \tan \beta =\frac{x+2h}{AB}`

[∵ C´M = C´B + BM = x + h + h]

⇒ AB = (x + 2h) cot β ….(ii)

From (i) and (ii), we have

x cot α= (x + 2h) cot β

⇒ x(cot α– cot β) = 2h cot β

`\Rightarrow x( \frac{1}{\tan \alpha }-\frac{1}{\tan \beta })=\frac{2h}{\tan \beta }`

`\Rightarrow x( \frac{\tan \beta -\tan \alpha }{\tan \alpha \tan\beta } )=\frac{2h}{\tan \beta }`

`\Rightarrow x=\frac{2h\tan \alpha }{\tan \beta -\tan \alpha }`

Hence,

Height of the cloud = x + h

`=\frac{2h\tan \alpha }{\tan \beta -\tan \alpha }+h`

`=\frac{2h\tan \alpha +h\tan \beta -h\tan \alpha }{\tan \beta -\tan \alpha }`

`=\frac{h(\tan \alpha +\tan \beta )}{\tan \beta -\tan \alpha }`