Question

If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10

Answer 1

Let the coordinates of P be (x, y). Then,

PA = PB

`⇒ PA^2 = PB^2`

`⇒ (x – 3)^2 + (y– 4)^2 = (x – 5)^2 + (y + 2)^2`

⇒ x – 3y – 1 = 0 ….(1)

Now, Area of ∆PAB = 10

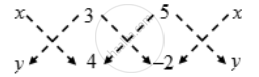
`⇒ \frac { 1 }{ 2 } |(4x + 3 × (–2) + 5y) – (3y + 20 – 2x)| = 10`

⇒ |(4x + 5y – 6) – (–2x + 3y + 20)| = 20

⇒ |6x + 2y – 26| = ± 20 ⇒ 6x + 2y – 26 = ± 20

⇒ 6x + 2y – 46 = 0 or, 6x + 2y – 6 = 0

⇒ 3x + y – 23 = 0 or, 3x + y – 3 = 0

Solving x – 3y – 1 = 0 and 3x + y – 23 = 0

we get x = 7, y = 2.

Solving x – 3y – 1 = 0 and 3x + y – 3 = 0,

we get x = 1, y = 0.

Thus, the coordinates of P are (7, 2) or (1, 0)