Question

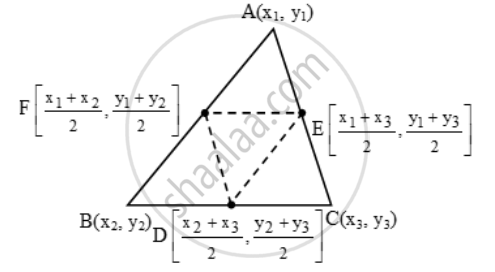
If D, E and F are the mid-points of sides BC, CA and AB respectively of a ∆ABC, then using coordinate geometry prove that Area of ∆DEF = `\frac { 1 }{ 4 } "(Area of ∆ABC)"`

Answer 1

Let `A(x_1 , y_1 ), B(x_2 , y_2 ) and C(x_3 , y_3 )`be the vertices of ∆ABC. Then, the coordinates of D, E and F are

`((x_2+x_3)/2,(y_2+y_3)/2)((x_1+x_3)/2,(y_1+ y_3)/2)((x_1+x_2)/2,(y_1+y_2)/2)`

`∆_1 = Area of ∆ABC = \frac { 1 }{ 2 } | x_1 (y_2 – y_3 ) + x_2 (y_3 – y_1 ) + x_3 (y_1 – y_2 ) |`

∆_2 = Area of ∆DEF

`=1/2|((x_2+x_3)/2)((y_1+y_3)/2-(y_1+y_2)/2)+((x_1+x_3)/2)((y_1+y_2)/2-(y_2+y_3)/2)+((x_1+x_2)/2)((y_2+y_3)/2-(y_1+y_3)/2)|`

`⇒ ∆_2 = \frac { 1 }{ 8 } |(x_2 + x_3 )(y_3 – y_2 ) + (x_1 + x_3 )(y_1 – y_3 ) + (x_1 + x_2 )(y_2 – y_1 )|`

`⇒ ∆_2 = \frac { 1 }{ 8 } |x_1 (y_1 – y_3 + y_2 – y_1 ) + x_2 (y3 – y_2 + y_2 – y_1 ) + x_3 (y_3 – y_2 + y_1 – y_3 )|`

`⇒ ∆_2 = \frac { 1 }{ 8 } |x_1 (y_2 – y_3 ) + x_2 (y_3 – y_1 ) + x_3 (y_1 – y_2 )|`

`⇒ ∆_2 = \frac { 1 }{ 4 } (`

Hence, Area of ∆DEF = `\frac { 1 }{ 4 } "(Area of ∆ABC)"`