Question

If d₁, d₂ (d₂ > d₁) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______ 

Options

• d₂² = c² + d₁²

• d₂² = c² - d₁²

• d₁² = c² + d₂²

• d₁² = c² - d₂²

Answer 1

If d₁, d₂ (d₂ > d₁) be the diameters of two concentric circles and c be the length of a chord of a circle that is tangent to the other circle, then d₂² = c² + d₁².

Explanation:

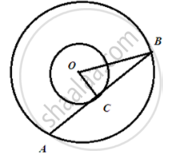
Let AB be a chord of a circle that touches the other circle at C. Then ΔOCB is the right triangle.

By Pythagoras theorem

OC² + CB² = OB²

⇒ `(1/2d_1)^2 + (1/2c)^2 = (1/2d_2)^2`

⇒ d₂² = c² + d₁²