Question

If I ask you to construct ΔPQR ~ ΔABC exactly (when we say exactly, we mean the exact relative positions of the triangles) as given in the figure, (Assuming I give you the dimensions of ΔABC and the Scale Factor for ΔPQR) what additional information would you ask for?

Options

• The information given is sufficient.

• We cannot construct the triangle because there is no connection between two triangles.

• Perpendicular distance between AC and Point P and angle between AC and PR.

• Dimensions of PQR.

Answer 1

Perpendicular distance between AC and Point P and angle between AC and PR.

Explanation:-

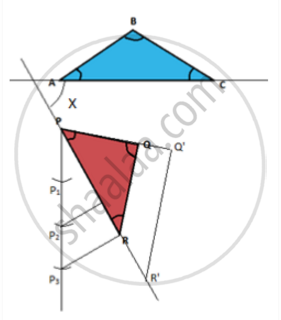
Consider we need to draw a triangle ΔPQR ~ ΔABC. But ΔPQR is at an isolated position w.r.t. ΔABC. Therefore we will need to know the perpendicular distance between AC and point P and the angle between AC and PR.

Now let us reframe the question with the required information.

Construct a triangle ΔPQR similar to ΔABC, such that point P is at a perpendicular distance 5cm from the line AC, PR makes an angle of 60° and which is 23rd of ΔABC. In triangle ΔABC, AB = 6 cm, AC = 7 cm, and ∠ABC = 30°

Steps of construction:

1. Draw a straight line AC = 7 cm.
2. Measure an angle of 30° w.r.t AC and draw a straight line
3. Set the compass at 6 cm length and with A as centre mark the length on the line, name the point of intersection as B.
   Reason: This is done to draw the line AB. i.e. we are marking the length of 6 cm on the line 30° inclined to AC
4. Connect the points to BC to complete the triangle.
5. Draw a line perpendicular to AC at A.
   Reason: We are drawing this step to identify the line on which the point P might lie.
6. For the given length of AP, cut the perpendicular at P Reason: We are drawing the arc to identify the exact position of point P on the line perpendicular to AC
7. Extrapolate line segment AC. Reason:
8. Draw a Ray XY 60° to AC, such that the line passes through the point P.
9. Measure the distance AC with a compass and draw an arc with point P as centre and radius equal to AC, the point of intersection is R’.
10. Measure z.BAC and draw a similar angle on PR’.
11. Measure AB and mark on PZ as PQ. Join QR’.
12. Draw a ray PM, mark 3 points P₁P₂P₃ such that PP₁=P₁P₂=P₂P₃
13. Join R′P₃
14. Through P2 draw a line parallel to P3R′, let the point of intersection of the line with PR’ is R.
15. Through the point R, draw a line parallel to R’Q’. Let the point of intersection of the line with line PO! is Q. The triangle ΔPQR which is similar to and ΔABC such that, the angle between PR and AC is 120° and perpendicular distance of point P from AC is 5 cm.