Advertisements
Advertisements
Question
If θ is the acute angle between the vectors `hati + hatj + hatk` and `2hati - hatj + hatk`, then tan θ is ______.
Options
`7/2`
`sqrt(7)/2`
`sqrt(7/2)`
`2/sqrt(7)`
MCQ
Fill in the Blanks
Solution
If θ is the acute angle between the vectors `hati + hatj + hatk` and `2hati - hatj + hatk`, then tan θ is `underlinebb(sqrt(7/2))`.
Explanation:
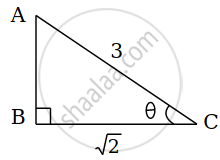
Let `bara = hati + hatj + hatk`,
`barb = 2hati - hatj + hatk`
∴ `bara*barb` = (1)(2) + (1)(–1) + (1)(1)
= 2 – 1 + 1
= 2
`|bara| = sqrt(1 + 1 + 1)`
= `sqrt(3)`,
`|barb| = sqrt(4 + 1 + 1)`
= `sqrt(6)`
cos θ = `(bara*barb)/(|bara||barb|)`
= `2/(sqrt(3)sqrt(6))`
= `2/(3sqrt(2))`
= `sqrt(2)/3`
cos θ = `(BC)/(AC)`
= `sqrt(2)/3`
∴ (AB)2 = (AC)2 – (BC)2
= 9 – 2
= 7
∴ AB = `sqrt(7)`
∴ tan θ = `(AB)/(BC)`
= `sqrt(7)/sqrt(2)`
= `sqrt(7/2)`
shaalaa.com
Scalar Product of Vectors (Dot)
Is there an error in this question or solution?
