Question

If one of the diameters of the circle x² + y² – 2x – 6y + 6 = 0 is a chord of another circle 'C' whose center is at (2, 1), then its radius is ______.

Options

• 0

• 1

• 2

• 3

Answer 1

If one of the diameters of the circle x² + y² – 2x – 6y + 6 = 0 is a chord of another circle 'C' whose center is at (2, 1), then its radius is 3.

Explanation:

Given: One of the diameters of the circle x² + y² – 2x – 6y + 6 = 0 is a chord of another circle C whose center is at (2, 1).

Compare given equation of circle with x² + y² + 2gx + 2fy + c = 0

g = –1, f = –3, c = 6

Center ≡ C₁(–g, –f) ≡ C₁(1, 3)

Radius = `sqrt("g"^2 + "f"^2 - "c")`

r₁ = `sqrt((-1)^2 + (-3)^2 - 6)` = 2

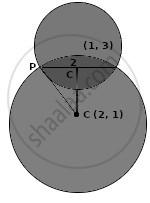
Let center of another circle is C

Midpoint of chord coincides with center C₁

Distance between C and C₁

= `sqrt((2 - 1)^2 + (1 - 3)^2`

= `sqrt(1^2 + (-2)^2)`

CC₁ = `sqrt(5)`

PC² = `"C" "C"_1^2 + "r"_1^2`

= `(sqrt(5))^2 + 2^2`

= 5 + 4 = 9

PC = `sqrt(9)` = 3

Hence, required radius = 3