Question

If one of the diameters of the curve x² + y² - 4x - 6y + 9 = 0 is a chord of a circle with centre (1, 1), then the radius of this circle is ______ 

Options

• 3

• 2

• `sqrt2`

• 1

Answer 1

If one of the diameters of the curve x² + y² - 4x - 6y + 9 = 0 is a chord of a circle with centre (1, 1), then the radius of this circle is 3. 

Explanation:

Given the equation of a circle is

x² + y² - 4x - 6y + 9 = 0

⇒ x² - 4x + 4 + y² - 6y + 9 - 4 = 0

⇒ (x - 2)² + (y - 3)² = 4

∴ centre = (2, 3), radius = 2

The diameter of this circle is a chord of a circle with a centre O(1, 1).

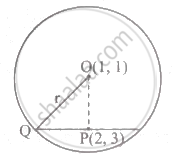
OP = `sqrt((3 - 1)^2 + (2 - 1)^2) = sqrt5`

QP = 2

∴ `r^2 = (sqrt(5))^2 + 2^2 ⇒ r = 3`