Advertisements
Advertisements
Question
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
Solution
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
≡ ~ [T ∨ (F ∧ F)] ∧ ~ [(F ∧ ~ F) ∧ T]
≡ ~ (T ∨ F) ∧ ~ [(F ∧ T) ∧ T]
≡ ~ T ∧ ~ (F ∧ T)
≡ F ∧ ~ F
≡ F ∧ T
≡ F
Hence, truth value is F.
APPEARS IN
RELATED QUESTIONS
Using the truth table, prove the following logical equivalence :
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Write converse, inverse contrapositive of the statement "If two triangles are not congruent then their areas are not equal.
Write the following compound statement symbolically.
x is not irrational number but is a square of an integer.
Construct the truth table of the following statement pattern.
(q → p) ∨ (∼ p ↔ q)
Construct the truth table of the following:
∼ (∼p ∧ ∼q) ∨ q
Express the following statement in symbolic form.
Mango is a fruit but potato is a vegetable.
Express the following statement in symbolic form.
I like playing but not singing.
Write the truth value of the following statement.
The Himalayas are the highest mountains but they are part of India in the North East.
Write the truth value of the negation of the following statement.
For every x ∈ N, x + 3 < 8.
Write the following statement in symbolic form.
It is not true that “i” is a real number.
Write the following statement in symbolic form.
Even though it is not cloudy, it is still raining.
Write the following statement in symbolic form.
Stock prices are high if and only if stocks are rising.
Find the truth value of the following statement.
It is not true that 3 − 7i is a real number.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
p ↔ ~ q
Fill in the blanks :
Conjunction of two statement p and q is symbolically written as ______.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The Sun has set and Moon has risen.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Mona likes Mathematics and Physics.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that Ram is tall and handsome.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Even though it is not cloudy, it is still raining.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∨ r
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
∼ p ∨ q
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → q
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If demand falls, then price does not increase.
Write the negation of the following.
An angle is a right angle if and only if it is of measure 90°.
If p → q is an implication, then the implication ∼ q → ∼ p is called its
Using truth table prove that p ˅ (q ˄ r) ≡ (p ˅ q) ˄ (p ˅ r)
Choose the correct alternative:
Negation of p → (p ˅ ~q) is
Write the negation of the statement “An angle is a right angle if and only if it is of measure 90°”
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
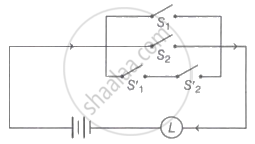
Let p : 7 is not greater than 4 and q : Paris is in France by two statements. Then ∼(p ∨ q) is the statement ______
Which of the following is NOT true for p → q.
Write the converse, inverse, and contrapositive of the statement. "If 2 + 5 = 10, then 4 + 10 = 20."
Which of the following is logically equivalent to `∼(∼p \implies q)`?
Write the following statement in symbolic form.
4 is an odd number if 3 is not a prime factor of 6.
If p, q are true statements and r, s are false statements, then write the truth value of the compound statement
(p `→` ∼ r) `→` (q ∧ s)
Using truth table prove that:
~ (p `leftrightarrow` q) ≡ (p ∧ ~ q) ∨ (q ∧ ~ p)
