Advertisements
Advertisements
Question
If `p(x) = x^2 - 2sqrt(2)x + 1`, then `p(2sqrt(2))` is equal to ______.
Options
0
1
`4sqrt(2)`
`8sqrt(2) + 1`
Solution
If `p(x) = x^2 - 2sqrt(2)x + 1`, then `p(2sqrt(2))` is equal to 1.
Explanation:
Given, `p(x) = x^2 - 2sqrt(2)x + 1` ...(i)
On putting `x = 2sqrt(2)` in equation (i), we get
`p(2sqrt(2)) = (2sqrt(2))^2 - (2sqrt(2))(2sqrt(2)) + 1`
= 8 – 8 + 1
= 1
APPEARS IN
RELATED QUESTIONS
Verify whether the following zeroes of the polynomial, indicated against them.
p(x) = (x + 1) (x – 2), x = – 1, 2
Find the zero of the polynomial in the following case:
p(x) = x – 5
Find the zero of the polynomial in the following case:
p(x) = 3x
Verify whether the indicated numbers is zeroes of the polynomials corresponding to them in the following case:
`f ( x ) = 3x +1, x = - 1/3`
If `x = −1/2` is a zero of the polynomial `p(x)=8x^3-ax^2 -+2` find the value of a.
Verify whether the following are zeros of the polynomial, indicated against them, or not
p(x) = ax + b, x = `(-"b")/"a"`
Find the number of zeros of the following polynomial represented by their graph
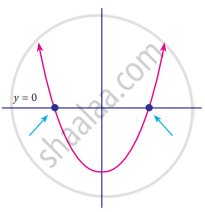
Find the number of zeros of the following polynomial represented by their graph
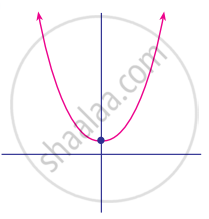
Zero of the zero polynomial is ______.
Find the zeroes of the polynomial in the following:
p(x) = x – 4
