Advertisements
Advertisements
Question
If R is any point on the x-axis and Q is any point on the y-axis and P is a variable point on RQ with RP = b, PQ = a. then find the equation of locus of P
Solution
P = (x, 0)
Q = (0, y)
R (h, k) be a point on RQ such that PR : RQ = b : a
∴ P = `(("a"x)/("a" + "b"), ("b"y)/("a" + "b"))`
⇒ `(("a"x)/("a" + "b"), ("b"y)/("a" + "b"))` = (h, k)
⇒ ax = (a + b)h
⇒ x = `("a" + "b")/"a" "h"`
by = (a + b)k
⇒ y = `("a" + "b")/"b" "k"`
From the right angled triangle OQR, OR2 + OQ2 = QR2 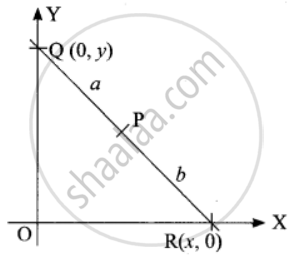
(i.e) X2 + Y2 = (a + b)2
⇒ `[("a" + "b")/"a" "h"]^2 + [("a" + "b")/"b" "k"]^2` = (a + b)2
⇒ `("a" + "b")^2/"a"^2 "h"^2 + ("a" + "b")^2/"b"^2 "k"^2` = (a + b)2
÷ by (a + b)2, `"h"^2/"a"^2 + "k"2/"b"^2` = 1
Locus is `x^2/"a"^2 + y^2/"b"^2` = 1
APPEARS IN
RELATED QUESTIONS
Find the locus of P, if for all values of α, the co-ordinates of a moving point P is (9 cos α, 9 sin α)
Find the locus of P, if for all values of α, the co-ordinates of a moving point P is (9 cos α, 6 sin α)
Find the locus of a point P that moves at a constant distant of two units from the x-axis
If θ is a parameter, find the equation of the locus of a moving point, whose coordinates are x = a cos3θ, y = a sin3θ
Find the value of k and b, if the points P(−3, 1) and Q(2, b) lie on the locus of x2 − 5x + ky = 0
Find the equation of the locus of the point P such that the line segment AB, joining the points A(1, −6) and B(4, −2), subtends a right angle at P
If O is origin and R is a variable point on y2 = 4x, then find the equation of the locus of the mid-point of segment OR
The coordinates of a moving point P are `("a"/2 ("cosec" theta + sin theta), "b"/2 ("cosec" theta - sin theta))` where θ is a variabe parameter. Show hat the equation of the locus P is b2x2 – a2y2 = a2b2
If P(2, – 7) is given point and Q is a point on 2x2 + 9y2 = 18 then find the equations of the locus of the midpoint of PQ
If Q is a point on the locus of x2 + y2 + 4x – 3y +7 = 0, then find the equation of locus of P which divides segment OQ externally in the ratio 3 : 4 where O is origin
Find the points on the locus of points that are 3 units from x-axis and 5 units from the point (5, 1)
The sum of the distance of a moving point from the points (4, 0) and (−4, 0) is always 10 units. Find the equation of the locus of the moving point
Choose the correct alternative:
Which of the following equation is the locus of (at2, 2at)
Choose the correct alternative:
Which of the following point lie on the locus of 3x2 + 3y2 – 8x – 12y + 17 = 0
