Question

If x + y + k = 0 touches the circle x² + y² - 2x - 4y + 3 = 0, then k will be ______

Options

• -1, 5

• 1, -5

• 1, 5

• -1, -5

Answer 1

If x + y + k = 0 touches the circle x² + y² - 2x - 4y + 3 = 0, then k will be -1, -5.

Explanation:

Comparing the given equation with

x² + y² + 2gx + 2fy + c = 0, we get

g = -1, f = -2, c = 3

∴ Centre = (1, 2), Radius = `sqrt(1 + 4 - 3) = sqrt2`

 

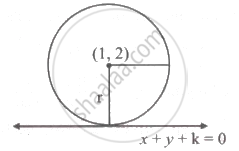
Since x + y + k = 0 touches the given circle,

`|(1 + 2  + k)/sqrt(1 + 1)|` = radius

⇒ `(3 + k)/sqrt2 = ±sqrt2`

⇒ k = -1 or k = -5