Question

If z = ax + by; a, b > 0 subject to x ≤ 2, y ≤ 2, x + y ≥ 3, x ≥ 0, y ≥ 0 has minimum value at (2, 1) only, then ______.

Options

• a > b

• a = b

• a < b

• a = 1 + b

Answer 1

If z = ax + by; a, b > 0 subject to x ≤ 2, y ≤ 2, x + y ≥ 3, x ≥ 0, y ≥ 0 has minimum value at (2, 1) only, then a < b.

Explanation:

We have, z = ax + by; a, b > 0

Subject to constraints x ≤ 2, y ≤ 2, x + y ≥ 3, x ≥ 0, y ≥ 0

On taking given constraints as equation, we get the following graph

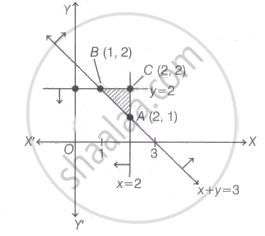
Here, ABCA is the required feasible region whose corner points are A (2, 1), B (1, 2) and C(2, 2).

Since, It is given that z =ax+ by; a, b > 0 has minimum value at (2, 1).

∴ Value of z at (2, 1) < value of z at (1, 2)

⇒ 2a + b < a + 2b

⇒ a < b