Advertisements
Advertisements
Question
In a class, all students take part in either music or drama or both. 25 students take part in music, 30 students take part in drama and 8 students take part in both music and drama. Find the number of students who take part in only music
Solution
Let M be the set of all students take part in music.
Let D be the set of all students take part in drama.
n(M) = 25, n(D) = 30 and n(M ∩ D) = 8
By using Venn-diagram
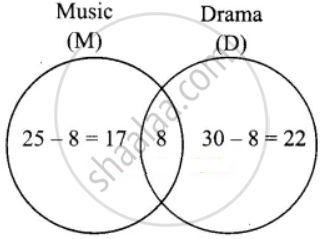
From the Venn-diagram we get.
Number of students take part in only music = 17
APPEARS IN
RELATED QUESTIONS
State, whether the pair of sets, given below, are equal sets or equivalent sets:
{7, 7, 2, 1,2} and {1, 2, 7}
State, whether the pair of sets, given below, are equal sets or equivalent sets:
{5, 5, 2, 4} and {5, 4, 2, 2}
Write the cardinal number of the following set:
E = {16, 17, 18 19}
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(B)
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(B ∪ D)
State true or false for the following. Correct the wrong statement.
If B = {1, 5, 51, 15, 5, 1}, then n(B) = 6.
In a class, all students take part in either music or drama or both. 25 students take part in music, 30 students take part in drama and 8 students take part in both music and drama. Find the total number of students in the class
A survey of 1000 farmers found that 600 grew paddy, 350 grew ragi, 280 grew corn, 120 grew paddy and ragi, 100 grew ragi and corn, 80 grew paddy and corn. If each farmer grew atleast anyone of the above three, then find the number of farmers who grew all the three.
In a class of 50 students, each one come to school by bus or by bicycle or on foot. 25 by bus, 20 by bicycle, 30 on foot and 10 students by all the three. Now how many students come to school exactly by two modes of transport?
If n(A ∪ B ∪ C) = 100, n(A) = 4x, n(B) = 6x, n(C) = 5x, n(A ∩ B) = 20, n(B ∩ C) = 15, n(A ∩ C) = 25 and n(A ∩ B ∩ C) = 10, then the value of x is
