Advertisements
Advertisements
Question
In a hexagon ABCDEF, side AB is parallel to side FE and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3. Find ∠B and ∠D.
Solution
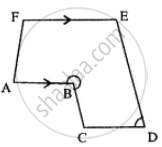
Given: Hexagon ABCDEF in which AB || EF and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3.
To find: ∠B and ∠D
Proof: No. of. sides n = 6
∴ Sum of interior angles = (n - 2) × 180°
= (6 - 2) × 180°
= 720°
∵ AB || EF (Given)
∴ ∠A + ∠F = 180°
But ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720° (Proved)
∠B + ∠C + ∠D + ∠E + 180° = 720°
∴ ∠B + ∠C + ∠D + ∠E = 720° - 180°
Ratio = 6: 4: 2: 3
Sum of parts = 6 + 4 + 2 + 3 = 15
∴ ∠B = `6/15 xx 540 = 216^circ`
∠D = `2/15 xx 540^circ = 72^circ`
Hence ∠B = 216° ; ∠D = 72°
APPEARS IN
RELATED QUESTIONS
Calculate the sum of angle of a polygon with: 10 sides
Calculate the sum of angle of a polygon with: 20 sides
Find the number of sides in a polygon if the sum of its interior angle is: 16 right-angles.
Find the number of sides in a polygon if the sum of its interior angle is: 32 right-angles.
Is it possible to have a polygon, whose sum of interior angle is: 2340°
Is it possible to have a polygon, whose sum of interior angle is: 7 right-angles
Is it possible to have a polygon, whose sum of interior angle is: 4500°
The interior angles of a pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Find each angle of the pentagon.
Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.
In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3 : 7. Find the biggest angle of the pentagon.
