Question

In a quadrilateral ABCD, M and N are the mid-points of the sides AB and CD respectively. If AD + BC = tMN, then t = ____________.

Options

• 2

• `1/2`

• 4

• `3/2`

Answer 1

In a quadrilateral ABCD, M and N are the mid-points of the sides AB and CD respectively. If AD + BC = tMN, then t = 2.

Explanation:

Given, In quadrilateral ABCD

M and N are the mid-point of side AB and CD.

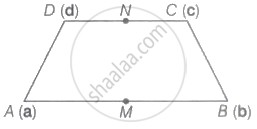
Let a, b, c and d are position vectors A, B, C and D respectively.

∴ M = `("a" + "b")/2`, N = `("c" + "d")/2`

∴ AD = d − a, BC = c − b

MN = `("c" + "d")/2 - ("a" + "b")/2`

2MN = (d − a) + (c − b)

2MN = AD + BC

∴ t = 2