Question

In a sphere of radius r, a right circular cone of height h having maximum curved surface area is inscribed. The expression for the square of curved surface of cone is ______.

Options

• 2π²rh(2rh + h²)

• π²hr(2rh + h²)

• 2π²r(2rh² – h³)

• 2π²r²(2rh – h²)

Answer 1

In a sphere of radius r, a right circular cone of height h having maximum curved surface area is inscribed. The expression for the square of curved surface of cone is 2π²r(2rh² – h³).

Explanation:

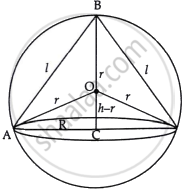
Here, CSA of cone = πRl

Radius of sphere = r

Height of cone = h

In ΔAOC,

AO² = AC² + OC²

`\implies` r² = R² + (h – r)²

`\implies` R² = 2hr – h²

∴ Radius of cone, `R = sqrt(2hr - h^2)`  ...(i)

In ΔABC,

AB² = AC² + BC²

`\implies` l² = R² + h²

`\implies` l² = 2hr – h² + h²

∴ Slant height = `sqrt(2hr)`  ...(ii)

CSA of cone = πRl

= `πsqrt(2hr - h^2) sqrt(2hr)`

(CSA of cone)² = π²(2hr – h²)(2hr)

= 2π²hr(2hr – h²)

= 2π²r(2rh² – h³)