Advertisements
Advertisements
Question
In a triangle ABC. If D is a point on BC such that ∠CAD = ∠B, then prove that: ∠ADC = ∠BAC.
Solution
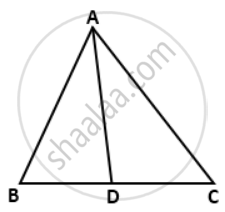
Given,∠CAD = ∠B ...(i)
By exterior angle property,
∠ADB = ∠CAD + ∠C
Also, ∠ADC = ∠BAD + ∠B
⇒ ∠ADC = ∠BAD + ∠CAD ....[From (i)]
⇒ ∠ADC = ∠BAC.
APPEARS IN
RELATED QUESTIONS
Use the given figure to find the value of x in terms of y. Calculate x, if y = 15°.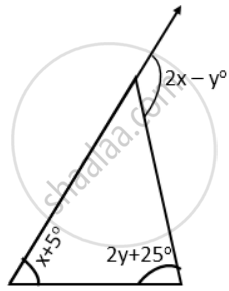
In a triangle PQR, ∠P + ∠Q = 130° and ∠P + ∠R = 120°. Calculate each angle of the triangle.
The angles of a triangle are (x + 10)°, (x + 30)° and (x - 10)°. Find the value of 'x'. Also, find the measure of each angle of the triangle.
Use the given figure to find the value of y in terms of p, q and r.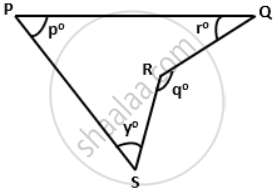
In the figure given below, if RS is parallel to PQ, then find the value of ∠y.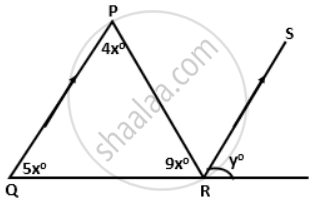
In a triangle ABC, if the bisectors of angles ABC and ACB meet at M then prove that: ∠BMC = 90° + `(1)/(2)` ∠A.
If bisectors of angles A and D of a quadrilateral ABCD meet at 0, then show that ∠B + ∠C = 2 ∠AOD
If the angles of a triangle are in the ratio 2: 4: 6; show that the triangle is a right-angled triangle.
In a triangle, the sum of two angles is 139° and their difference is 5°; find each angle of the triangle.
In a right-angled triangle ABC, ∠B = 90°. If BA and BC produced to the points P and Q respectively, find the value of ∠PAC + ∠QCA.
