Question

In a ∆ABC, AD ⊥ BC and AD² = BC × CD. Prove ∆ABC is a right triangle

Answer 1

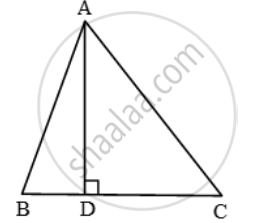
In right triangles ADB and ADC, we have

`AB^2 = AD^2 + BD^2 ….(i)`

and, `AC^2 = AD^2 + DC^2 ….(ii)`

Adding (i) and (ii), we get

`AB^2 + AC^2 = 2 AD^2 × BD^2 + DC^2`

`⇒ AB^2 + AC^2 = 2BD × CD + BD^2 + DC^2 [∵ AD2 = BD × CD `

`⇒ AB^2 + AC^2 = (BD + CD)^2 = BC^2`

Thus, in ∆ABC, we have

`AB^2 = AC^2 + BC^2`

Hence, ∆ABC, is a right triangle right-angled at A.