Question

In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`

Answer 1

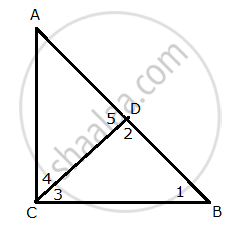
In Δ CDB,
`∠1 + ∠2 + ∠3 = 180º` 
`∠1 + ∠3 = 90º ...... (1)("Since", ∠2 = 90º)` 
`∠3 + ∠4 = 90º ...... (2) ("Since", ∠"ACB" = 90º)`
From (1) and (2),
`∠1 + ∠3 = ∠3 + ∠4`
`∠1 = ∠4`
`"Also", ∠2 = ∠5 = 90°`
`∴∆"BDC"  ~ ∆"CDA" ("By AA similarity")`
`⇒("DB")/("CD")=("CD")/("AD")`
`⇒"CD"^2= "AD"xx "DB"`