Question

In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.

Answer 1

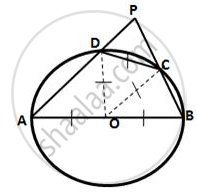
Join OD and OC.
ΔOCD, OD = OD= CD
∴ ΔOCD is an equilateral triangle
 ∴ ∠ODC =60°
Also, in cyclic quadrilateral ABCD
∠ADC + ∠ABC = 180°
(pair of opposite angles in cyclic quadrilateral are supplementary)
⇒ ∠ODA + 60° + ∠ABP =180°
⇒ ∠OAD + ∠ABP = 90° ( ∵  OA = OD)
⇒ ∠PAB = ∠ABP =120°
By angle sum property of ΔPAB,
∴ ∠APB = 180° - ∠PAB -∠ABP =180° -120°  =60°