Question

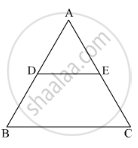
In Fig. 1, DE || BC, AD = 1 cm and BD = 2 cm. What is the ratio of the ar (Δ ABC) to the ar (Δ ADE)?

Answer 1

It is given that AD=1cm, BD=2 cm and DE||BC
In ΔADE and ΔABC
∠ADE = ∠ABC (corresponding angles)
∠A = ∠A (common angle)
By AA similarity
ΔADE - ΔABC

Ratio of area of similar triangles is equal to the square of the ratio of corresponding sides.

∴ `("ar"(Δ"ABC"))/("ar"(Δ"ADE")) = ("AB"^2)/("AD"^2)`

⇒ `("ar"(Δ"ABC"))/("ar"(Δ"ADE")) = (3^2)/(1^2)`

⇒ `("ar"(Δ"ABC"))/("ar"(Δ"ADE")) = (9)/(1)`

Therefore, the ratio of the ar (ΔABC) : ar (ΔADE) is 9 : 1.