Advertisements
Advertisements
Question
In fig. 7 is shown a disc on which a player spins an arrow twice. The fraction `a/b` is formed, where 'a' is the number of sector on which arrow stops on the first spin and 'b' is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction `a/b>1.`
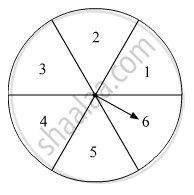
Solution
Elementary events associated with the experiment of spinning an arrow twice on a disc are
(1, 1), (1, 2), ...,(1, 6)
(2, 1), (2, 2), ...,(2, 6)
(3, 1), (3, 2), ...,(3, 6)
(4, 1), (4, 2), ...,(4, 6)
(5, 1), (5, 2), ...,(5, 6)
(6, 1), (6, 2), ...,(6, 6)
∴ Total number of elementary events = 36
It is given that a is the number of sector on which the arrow stops on the first spin and b is the number of the sector on which the arrow stops on the second spin.
Let A denote the event `a/b>1.`
Now,
`a/b>1Rightarrow a>b`
So, elementary events favourable to the event A are
(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4) and (6, 5)
∴ Total number of favourable events = 15
Thus,
Required probability =`"(The number of favourable events)"/"(Total number of the events)"=15/36 =5/12`
